최소값과 최대값 구하기

우리는 앞에서 min()과 max()를 이용하여 숫자들이 들어 있는 리스트에서 최소값과 최대값을 구할 수 있었습니다.

하지만 리스트에 숫자가 아닌 다른 종류의 데이터가 들어 있다면 일반적인 알고리즘을 알고 있어야 합니다.

리스트에 저장된 값들의 최대값이나 최소값을 어떻게 계산하는지 생각해봅시다.

예를 들어 우리는 인터넷에서 특정한 상품(예를 들면 레드벨벳 앨범)을 구입하고자 합시다.

여러 인터넷 사이트에서 판매되는 가격이 1차원 리스트 prices[]에 저장되어 있다고 가정했을 때 어떻게 하면 최소 가격으로 상품을 구입할 수 있을까요?

리스트 요소 중에서 최소값을 구하면 됩니다. 여기서 최소값을 구하는 알고리즘을 생각해봅시다.

 

최소값을 구할 때는 먼저 리스트의 첫 번째 요소를 최소값으로 가정합니다. 리스트의 두 번째 요소부터 마지막 요소까지 이 최소값과 비교합니다.

만약 어떤 요소가 현재의 최소값보다 작다면 새로운 최소값을 이것으로 변경하면 됩니다. 모든 요소들의 검사가 종료되면 최소값을 찾을 수 있습니다.

첫 번째 요소를 최소값 minimum이라고 가정합니다.
for i in range(1, 리스트의 크기):
	if ( s[i] < minimum ):
		minimum = s[i]
반복이 종료되면 minimum에 최소값이 저장됩니다.

 

최소값과 최대값을 계산하는 일반적인 알고리즘은 다음과 같습니다. 최소값을 계산한다고 가정합니다.

cheapest = prices[0]
for x in range(1, len(prices)):	# 0번째는 처리할 필요가 없습니다.
	if prices[i] < cheapest:
		cheapest = prices[i]

print("가장 싼 가격은 ", cheapest)

 

문자열이 저장된 리스트를 가정합시다. 가장 길이가 짧은 문자열을 찾으려고 합니다.

min()을 사용하면 알파벳 순서로 가장 앞에 있는 문자열을 반환합니다. 따라서 우리는 우리 나름대로의 코드를 작성해야 합니다.

words = ["cat", "mouse", "tiger", "lion"]
shortest = words[0]
for i in range(1, len(words)):
	if len(words[i]) < len(shortest):
		shortest = words[i]

print("가장 짧은 단어는", shortest)

 

<실행 결과>

가장 짧은 단어는 cat

 

탐색하기

아침에 입을 옷이나, 서랍 속에 있는 물건을 찾는 등 우리는 항상 무언가를 찾아 헤맵니다. 컴퓨터도 마찬가지입니다.

탐색(search)은 컴퓨터가 가장 많이 하는 작업 중의 하나입니다. 단순하게 우리가 인터넷에서 필요한 자료를 얼마나 많이 탐색하는지 생각하면 될 것입니다.

탐색은 많은 시간이 요구되는 작업이므로 효율적으로 수행하는 것은 매우 중요합니다.

 

 

탐색의 대상이 되는 데이터는 보통 리스트에 저장되어 있다고 가정합니다. 탐색이란 리스트에서 특정한 값을 찾는 것입니다.

리스트에서 탐색은 index() 메소드를 사용할 수 있습니다. index()는 리스트에서 항목을 찾아 항목의 인덱스를 반환합니다.

list = ["white", "silver", "blue", "red", "black"]
print(list.index("red"))

 

하지만 경우에 따라서 프로그래머가 탐색을 구현하여야 하는 경우도 있습니다. 따라서 우리는 탐색의 기본적인 방법을 알아둡시다.

여기서는 가장 간단한 알고리즘인 순차 탐색만 살펴보도록 할 것입니다. 순차 탐색(sequential search)은 탐색 방법 중에서 가장 간단하고 직접적인 탐색 방법입니다.

순차 탐색은 리스트의 요소를 순서대로 하나씩 꺼내서 탐색키와 비교하여 원하는 값을 찾아가는 방법입니다.

순차 탐색은 일치하는 항목을 찾을 때까지 비교를 계속합니다. 순차 탐색은 첫 번째 요소에서 성공할 수도 있고 마지막 요소까지 가야되는 경우도 있습니다.

평균적으로는 절반 정도의 리스트 요소와 비교하여야 할 것입니다.

 

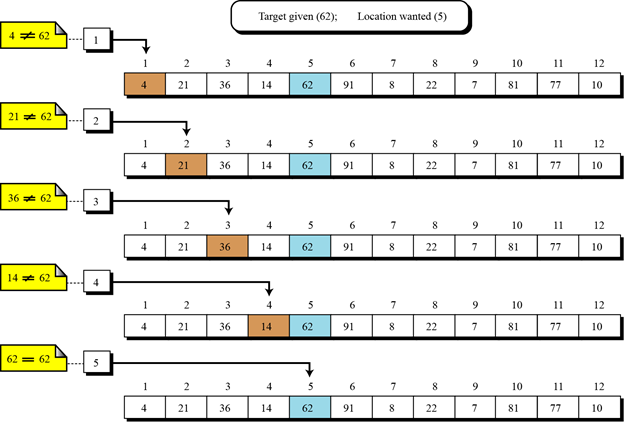
순차 탐색 알고리즘을 파이썬 함수로 표현하면 다음과 같습니다.

def linearSearch(aList, key):
	for i in range(len(aList)):
		if key == aList[i]:
			탐색을 성공했고 복귀합니다.
	복귀하지 않고 반복 루프가 종료되었으면 탐색 실패입니다.

 

순차 탐색 알고리즘을 파이썬으로 구현하고 테스트하는 코드는 다음과 같습니다.

def linearSearch(aList, key):
	for i in range(len(aList)):	# 리스트의 길이만큼 반복합니다.
		if key == aList[i]:		# 키가 발견되며 i를 반환하고 종료합니다.
			return i
	return -1					# 키가 발견되지 않고 반복이 종료되었으면 -1을 반환합니다.

numbers = [10, 20, 30, 40, 50, 60, 70, 80, 90]
position = linearSearch(numbers, 80)

if position != -1:
	print("탐색 성공 위치 = ", position)
else:
	print("탐색 실패")

 

<실행 결과>

탐색 성공 위치 =  7

 

조건을 만족하는 항목 모두 찾기

앞에서는 조건을 만족하는 첫 번째 요소의 위치만을 찾았습니다. 만약 조건을 만족하는 모든 요소를 찾으려면 어떻게 해야 할까요?

공백 리스트를 만들고 요소를 발견될 때마다 여기에 추가하면 쉽습니다. 리스트에서 50이 넘는 숫자들을 모두 찾는 코드는 아래와 같습니다.

numbers = [10, 20, 30, 40, 50, 60, 70, 80, 90]
result = []
for value in numbers:
	if value > 50:
		result.append(value)

print(result)

 

<실행 결과>

[60, 70, 80, 90]

 

파일을 읽어서 리스트에 저장하기

파일에서 데이터를 읽어 리스트에 저장하는 작업은 아주 많이 등장합니다. 기본적인 방법을 알아둡시다.

아래는 C:\temp 라는 폴더 경로 안에 data.txt 파일을 읽어 그 내용을 리스트에 추가 후 출력하는 예제입니다.

data = []
f = open("C:\temp\data.txt", "r")

# 파일에 저장된 모든 줄을 읽는다.
for line in f.readlines():
    # 줄바꿈 문자를 삭제한 후에 리스트에 추가한다.
    data.append(line.strip())

print(data)

 

정렬하기

정렬이란 리스트 안에 저장된 값을 순서에 따라서 나열하는 것입니다. 리스트에서 정렬은 sort() 메서도를 이용하여 쉽게 수행할 수 있습니다.

list = [3, 2, 1, 5, 4]
list.sort()

print(list)

 

<실행 결과>

[1, 2, 3, 4, 5]

 

하지만 경우에 따라서 우리가 정렬을 구현해야 하는 경우도 있습니다. 따라서 기본적인 방법은 알아둡시다.

선택 정렬은 가장 이해하기 쉬운 정렬 방법입니다. 먼저 두 개의 리스트가 있다고 가정합시다. 왼쪽에는 정렬된 리스트가 있고 오른쪽에는 정렬되지 않은 리스트가 있습니다.

초기 상태에서 정렬되어야 할 숫자들은 모두 정렬되지 않은 오른쪽 리스트에 들어 있습니다. 선택 정렬은 오른쪽 리스트를 탐색하여 가장 작은 숫자를 찾고 이 숫자를 왼쪽 리스트로 옮깁니다.

다음에 다시 오른쪽 리스트에 남아있는 숫자 중에서 다시 가장 작은 숫자를 찾아 왼쪽 리스트로 옮깁니다. 이 과정을 오른쪽 리스트가 공백 상태가 될 때까지 계속합니다.

 

설명	왼쪽 리스트	오른쪽 리스트
초기 상태	( )	(5, 3, 8, 1, 2, 7)
1 선택	(1)	(5, 3, 8, 2, 7)
2 선택	(1, 2)	(5, 3, 8, 7)
3 선택	(1, 2, 3)	(5, 8, 7)
5 선택	(1, 2, 3, 5)	(8, 7)
7 선택	(1, 2, 3, 5, 7)	(8)
8 선택	(1, 2, 3, 5, 7, 8)	( )

 

위의 방법을 구현하기 위해서는 입력 리스트와는 별도로 똑같은 크기의 리스트가 하나 더 필요합니다.

메모리를 절약하기 위하여 입력 리스트 외에 추가적인 공간을 사용하지 않는 선택 정렬 알고리즘을 생각해봅시다.

이렇게 입력 리스트 이외에는 다른 추가 메모리를 요구하지 않는 정렬 방법을 제자리 정렬(in-place) 이라고 합니다.

아래 그림에서 보면 하나의 최소값이 선택되고 왼쪽 리스트로 이동이 끝나면 오른쪽 리스트에 하나의 빈 공간이 생기는 것을 알 수 있습니다.

따라서 이것을 이용하도록 합시다. 즉 입력 리스트에서 최소값을 발견한 다음, 이 최소값을 리스트의 첫 번째 요소와 교환합시다.

다음에는 첫 번째 요소를 제외한 나머지 요소들 중에서 가장 작은 값을 선택하고 이를 두 번째 요소와 교환합시다.

이 절차를 리스트의 길이만큼 되풀이하면 전체 숫자들이 정렬됩니다.

 

 

# 선택 정렬을 구현하는 함수
def selectionSort(aList):
    for i in range(len(aList)):          # 리스트의 모든 요소에 대하여 반복
        least = i
        leastValue = aList[i]

        for k in range(i+1, len(aList)):
            if aList[k] < leastValue:    # k번째 요소가 현재의 최소값보다 작으면
                least = k                # k번째 요소를 최소값으로 합니다.
                leastValue = aList[k]

        tmp = aList[i]                   # i번째 요소와 최소값을 교환합니다.
        aList[i] = aList[least]
        aList[least] = tmp

list1 = [7, 9, 5, 1, 8]
selectionSort(list1)
print(list1)

 

<실행 결과>

[1, 5, 7, 8, 9]

 

도전 과제

요새 들어 자료구조 과제에 치여 기억력이 가물가물한 봉민이는 파이썬을 이용하여 지인의 연락처를 관리하는 프로그램을 작성하고자 합니다.

연락처 관리 프로그램의 실행 결과는 아래와 같습니다.

 

<실행 결과>

------------------------
1. 친구 리스트 출력
2. 친구 추가
3. 친구 삭제
4. 이름 변경
9. 종료
메뉴를 선택하세요 : 2
이름을 입력하세요 : 김봉민
------------------------
1. 친구 리스트 출력
2. 친구 추가
3. 친구 삭제
4. 이름 변경
9. 종료
메뉴를 선택하세요 : 1
['김봉민']
------------------------
1. 친구 리스트 출력
2. 친구 추가
3. 친구 삭제
4. 이름 변경
9. 종료
메뉴를 선택하세요 : 4
변경하려는 이름을 입력하세요 : 김봉민
새로운 이름을 입력하세요 : 강슬기
------------------------
1. 친구 리스트 출력
2. 친구 추가
3. 친구 삭제
4. 이름 변경
9. 종료
메뉴를 선택하세요 : 3
삭제하려는 이름을 입력하세요 : 김봉민
이름이 발견되지 않았습니다.
------------------------
1. 친구 리스트 출력
2. 친구 추가
3. 친구 삭제
4. 이름 변경
9. 종료
메뉴를 선택하세요 : 3
삭제하려는 이름을 입력하세요 : 강슬기
------------------------
1. 친구 리스트 출력
2. 친구 추가
3. 친구 삭제
4. 이름 변경
9. 종료
메뉴를 선택하세요 : 1
[]
------------------------
1. 친구 리스트 출력
2. 친구 추가
3. 친구 삭제
4. 이름 변경
9. 종료
메뉴를 선택하세요 : 9